اثری که به ساختار ظریف خط های طیف نشری اتم ها مربوط است ؛ توسّط زیمان در سال 1986 کشف شد و می توان آن را چنین بیان کرد . « هرگاه اتم هیدروژن ، در یک میدان مغناطیسی مناسب قرار گیرد ، طیف نشری آن به مراتب پیچیده تر از هنگامی می شود که در بیرون از میدان مغناطیسی به دست می آید . یعنی ، هرخط طیفی که در بیرون از میدان مغناطیسی قابل مشاهده باشد ، در میدان مغناطیسی مطابق شکل زیر :
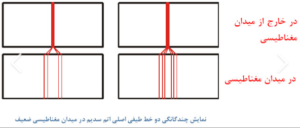 به صورت چند خط ظریف طیفی که به یکدیگر بسیار نزدیکند و به فاصله برابر قرار دارند ، دیده می شوند . و به اصطلاح طیف اتم ساختار ظریفی پیدا می کند .
به صورت چند خط ظریف طیفی که به یکدیگر بسیار نزدیکند و به فاصله برابر قرار دارند ، دیده می شوند . و به اصطلاح طیف اتم ساختار ظریفی پیدا می کند .
فاصله این خط ها ( یا تفاوت فرکانس یا طول موج آنها ) به شدّت میدان مغناطیسی بستگی دارد . برای توجیه این اثر با توجه به این که ظهور هر خط طیفی نشانه وجود دو تراز انرژی مجزّا از یکدیگر است باید پذیرفت که یک تراز فرعی ( که انرژی آن با عدد کووانتومی l مشخص می شود . )می بایست شامل چند تراز فرعی انرژی بسیار نزدیک به هم باشد که هریک از آنها ، منشاء ظهر یک خط طیفی ظریف است . برای این منظور ، باید برای حرکت الکترون به دور هسته ، یک درجه آزادی دیگر در نظر گرفت . از آن جایی که الکترون ذره ای باردار است و ضمن چرخش به دور هسته ، حکم یک مغناطیس کوچک را دارد ، پس صفحه چرخش آن در ترازهای فرعی مانند یک صفحه مغناطیسی ، تحت تاثیر میدان مغناطیسی بیرونی واقع شده و بر اثر یک جفت نیرو در راستای معینی قرار می گیرد که با راستای میدان ( بر اساس شکل زیر ) زاویه \( \theta \) تشکیل می دهد .مقدار این زاویه باید از شرط کووانتومی بون پیروی کند به طوری که تصویر اندازه حرکت الکترون به دور هسته بر روی تراز فرعی l( یعنی \( I^{\to }=mvr \)بر روی راستای میدان مغناطیسیH ، مضرب درستی از واحد بنیادی کووانتوم( \( \frac{h}{2\pi} \)) باشد .
این مضرب درست را معمولاً با \( m_{e} \)نشان می دهند که عدد کووانتومی مغناطیسی نامیده می شود ، از این رو می توان نوشت :\( \overline{OM}=m_{l}\frac{h}{2\pi} \)
چون داریم :\( \overline{OM}=\overrightarrow{l}cos\theta \)و طبق نظریه سامرفلد مقدار \( \overrightarrow{l} \)برابر \( l\frac{h}{2\pi} \)است .
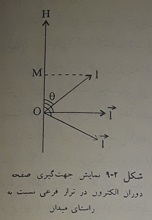 با توجه به تصویر می توان نوشت :\( \overrightarrow{l}cos\theta=l\frac{h}{2\pi}cos\theta\\l\frac{h}{2\pi}cos\theta=m_{l}\frac{h}{2\pi}\\ lcos\theta=m_{l}\\ \frac{m_{l}}{l}=cos\theta \)
با توجه به تصویر می توان نوشت :\( \overrightarrow{l}cos\theta=l\frac{h}{2\pi}cos\theta\\l\frac{h}{2\pi}cos\theta=m_{l}\frac{h}{2\pi}\\ lcos\theta=m_{l}\\ \frac{m_{l}}{l}=cos\theta \)
با توجه به حد ّ \( cos\theta \)که بین 1+ و 1- است ، داریم : \( -1\leqslant \frac{m_{l}}{l}\leqslant 1 \) و یا \( m_{l}=-1 ,0,+1 \) یعنی اگر l=0 باشد ، مقدار \( m_{l}=0 \)است و تراز فرعی ( زیرلایه ) تنها شامل یک تراز فرعی تر ( تراز S) است . اگر l=1 باشد ، ( تراز P ) ، \( m_{l} \) می تواند سه مقدار 1+ ، 0 و 1- را داشته باشد یعنی شامل اوربیتال ( اوربیتال های \( P_{z}, P_{y}, P_{x} \) ) است و …..
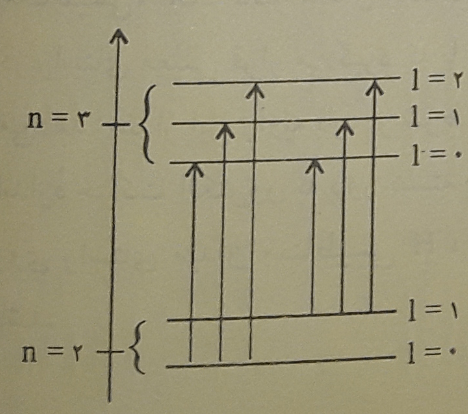
بر این اساس ، می توان برای نمونه ، شش جهش الکترونی را بین ترازهای اصلی دوم و سوم پیشگویی کرد :

از این رو ، الکترون در جهش و سقوط بین دو تراز فرعی ، بسته به این که از کدام اوربیتال تراز فرعی به کدام اوربیتال تراز فرعی دیگر در میدان مغناطیسی جهش و سقوط کند با توجه به اصل های انتخاب ، چندین خط طیفی ظریف نزدیک به هم در طیف آن آشکار می شود . بدین ترتیب اثر زیمان به روشنی توجیه شده است .
پیتر زیمان ، فیزیکدان هلندی که در سال 1865 در زونمر از ایالت زیلاند زاده شد . در دانشگاه لیدن زیر نظر کامرینگ اونس و لورنتس تحصیل کرد . در اثر راهنمایی های لورنتس ، آزمایش هایی در مورد تاثیر میدان مغناطیسی بر هر نوری که از آن بگذرد ، انجام داد و در سال 1869 آنچه را اکنون به « اثر زیمان » مشهور است و تاییدی بر گفته ها و نظریه لورنتس بود ، کشف کرد . زیمان در سال 1943 در آمستردام ( هلند ) از دنیا رفت .



برای نوشتن دیدگاه باید وارد بشوید.